Pythagorean theology: Truth in numbers

In their quest for the ultimate symbols to represent reality the Greeks developed a theological system that although was analogous to the pantheistic tradition within which it coexisted, was relatively independent from it and was perceived to be, at least by the Greek philosophers, ontological prior to the system of gods and goddesses that were wrapped in the myth of history.

The practice of what we might call numerology – numbers, mathematics and even geometry as theological symbols – begins, at least in the Greek philosophical tradition, with Pythagoras (c. 570 – 490 BCE), whose strong connection to mathematics survives even to this day with his continued association with the Pythagorean theorem for example. But much of the philosophical and mystical aspects of the Pythagorean school are somewhat lost by modern academics and scholars who look for a specific documented philosophical position to attribute to him and/or his followers. If he wrote anything it doesn’t survive, and although he is frequently mentioned in the writings of Aristotle and Plato he’s not given much credit for any particular philosophical position or cosmology, outside of the attribution of mathematics, and numbers specifically, as a window into the cosmic world order, a mathematical world order that governed not only earthly activities and the disposition and behavior of man, but also the behavior and functioning of the celestial and heavenly world order – again following the presupposition that in man could be found the mirror of the cosmos at large.

The problem with trying to truly understand the philosophy of Pythagoras is that the literature regarding who he was and what he believed and taught only survives from (direct) sources that wrote some five or six centuries after his death at least – with the Neo-Platonists Iamblichus (c. 245 – 325 CE) and Porphyry (234 – c. 305 CE) as well as the historian Diogenes Laertius (c. 200-250 CE) being perhaps the best full accounts of his life that still extant although we do have several contemporaneous references to him beyond just Plato and Aristotle such as Herodotus (c. 484 – 425 BCE) for example, speaking to how well known he was in his time.

What we do know is that before he settled to teach in Italy to teach he traveled widely and spent a good deal of time in Egypt, being initiated into one the priestly sects there, and most likely spent time studying in the Near East as well given his school’s deep associations with ritual, dietary restrictions, and reincarnation. What is clear however is that for Pythagoras and his followers, numbers and their relationships – i.e. geometry – was a sacred science which facilitated knowledge of human as well as celestial affairs and governed the world order.

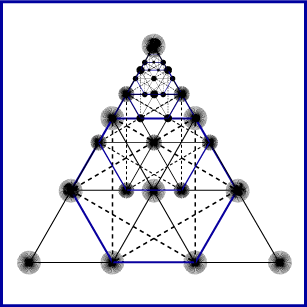
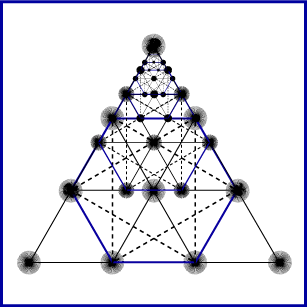
To the Pythagoreans, each of the numbers from 1 to 10 had specific and significant esoteric and metaphysical meanings above and beyond simple numbers that were used for calculation. The One, or the Monad, represented the indivisible source of all things, unity and perfection. Two, or the Dyad, represented opposition or inequality and was the first element in the creative process of the universe from the Monad. The Triad, or the number three, represented wholeness and knowledge, the powers of prophecy and fate, and was reflected in the tripartite Soul[1]. The Tetrad, of the number four, represented completion and was reflected in the four elements and the four seasons as well as the four mathematical sciences of arithmetic, music, geometry and astronomy. This number four, or the first four numbers in fact, came to be representative of the Pythagorean cosmic order and was reflected in their most sacred symbol the tetraktys, a triangular figure that consists of 10 points, with a base of 4, then 3, then 2, then 1 points, synthesizing their numerological philosophy and coming to be representative of their philosophy as a whole in antiquity.

Probably the best source of the content of Pythagorean philosophy outside of Plutarch, Diogenes Laertius and Porphyry who all write some 6 or 8 centuries after Pythagoras lives and after the tradition surrounding him takes on somewhat mythical status, is Aristotle who writes the following brief synopsis of Pythagoras’s philosophical principles in Metaphysics Book I as he surveys the philosophical landscape prior to laying out his own alternative metaphysical framework:

Contemporaneously with these philosophers and before them, the so-called Pythagoreans, who were the first to take up mathematics, not only advanced this study, but also having been brought up in it they thought its principles were the principles of all things. Since of these principles numbers are by nature the first, and in numbers they seemed to see many resemblances to the things that exist and come into being-more than in fire and earth and water (such and such a modification of numbers being justice, another being soul and reason, another being opportunity-and similarly almost all other things being numerically expressible); since, again, they saw that the modifications and the ratios of the musical scales were expressible in numbers;-since, then, all other things seemed in their whole nature to be modeled on numbers, and numbers seemed to be the first things in the whole of nature, they supposed the elements of numbers to be the elements of all things, and the whole heaven to be a musical scale and a number. And all the properties of numbers and scales which they could show to agree with the attributes and parts and the whole arrangement of the heavens, they collected and fitted into their scheme; and if there was a gap anywhere, they readily made additions so as to make their whole theory coherent. E.g. as the number 10 is thought to be perfect and to comprise the whole nature of numbers, they say that the bodies which move through the heavens are ten, but as the visible bodies are only nine, to meet this they invent a tenth–the ‘counter-earth’. We have discussed these matters more exactly elsewhere.[2]

The true legacy of Pythagoras then is sacred geometry, the notion that basic mathematical principles were a reflection of the divine and by contemplating them one could come to know, have knowledge of, the Monad, the source of all things. From this association we are left with not just the Pythagorean theorem whose discovery is ascribed to him[3], but also the sacred symbol tetraktys which sums up his esoteric philosophy in symbolic form.

While there is reason to believe that Pythagorean philosophy may have been more an amalgamation and synthesis of Egyptian, Babylonian, Chaldean and Magian (Persian) elements rather than a new and unique philosophical system per se, what can be said about Pythagoras is that he is absolutely instrumental in introducing philosophy as a practice in and of itself to the Greek populace in general, with words such as kosmos and philosophía first use being attributed to him as well.