Sacred Geometry in Plato’s Timaeus

After Pythagoras, the next in line in the propagation of core mathematical constructs, not just numbers themselves but again geometry as well, as key elements of the universal world order, is Plato.  It is said that outside of the Academy which was founded by Plato was inscribed “Let no one ignorant of geometry enter”, and although whether or not the inscription actually existed cannot be confirmed, it is very well consistent with the philosophical system that Plato sets out in his dialogues, especially the Republic and the Timaeus which cover his Theory of Forms, its relationship to numbers and mathematics in general, and his theory of Platonic solids which underlies his physical cosmology.

And particularly with the Platonic school, believed to have been influenced by the Pythagoreans who preceded them, we see a prominent role for numerology and geometry that is hinged not onto the cosmological and physical view of the school – how the universe came to be and is maintained – but how the universe itself in all its grand mystery could be understood.  The gift of mathematics, geometry, as a sacred science was not invented by the Greeks no doubt, but its emphasis along with much of its breadth and early explanation, is a legacy of the Greeks.

The influence of mathematics and numerology on Plato’s philosophy can probably best be seen by later interpreters of his works, as his Being and Becoming, and his notion of the Good which represents the Form of Forms is transformed into the One of the Neo-Platonic tradition, the principle being very squarely aligned with the Pythagorean Monad.  Furthermore, in interpretations of passages in the Republic, reference to numerical and mathematical constructs as things that can be conceived of only in thought, i.e. examples of Forms or Ideas[1].

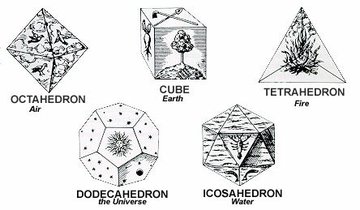
In Plato’s Timaeus we have a more systematic outlining of the role of mathematics and geometry in the universal world order.  Here we can find not only some traces of Pythagorean thought (as much emphasis is given to the role of triangles in the formulation and construction of the physical world, one of which is Pythagorean so to speak) as well as the role of geometry in general as he outlines a core set of geometric shapes which have come to be known as Platonic solids that form the basic shape and building blocks of the four primary elements – earth, air, water, fire – from which the physical universe is constructed.

In the Timaeus Plato describes a universe that is living in and of itself, i.e. the World Soul, which is governed by a fundamental order, i.e. Pythagoras’s kosmos.  The universal order that Plato speaks of one which akin to eternal Being but yet is in motion, and is governed by time which in turn is governed by number and basic mathematical principles.  This concept of time, its association with number and the movement of the heavenly bodies themselves, is a core characteristic of the World Soul, the universe, and is one of the key attributes of the kosmos itself.

Plato further outlines a hierarchy of beings in the kosmos, one which sits with the Demiurge at the top of the hierarchy and under him you have the various gods who are associated with the heavens and then the world of mortals which are manufactured by the gods, all of which are created via the Demiurge and which represent manifestations of nous, or the intellect of the Demiurge, a principle which came to be known as Intellect itself in later Neo-Platonic interpretations of the Timaeus and which encapsulated the world of Forms and Ideas which represented the core of Plato’s metaphysics[2]. 

In Plato’s “likely account” (eikôs logos) or “likely story” (eikôs muthos) of the universal creation described in the Timaeus, the Demiurge or World Soul, fashions the corporeal world from the two primordial substances of the universe – what are referred to by most translators as the “Same” and the “Other” denoting one’s (the Same) indivisible nature and the Other’s divisible nature – and an intermediary substance between the two and created two great circles, the outer of which he made the motion of the Same and the inner of which he made the motion of the Other, each moving in opposite directions.  The inner circle he then split into seven parts to yield the 7 celestial spheres, or 8 counting the outermost sphere of the fixed stars, i.e. the circle of the Same.[3]

After the model itself and its motion has been established, Plato then places the divine creatures themselves, i.e. the gods, planets (“wanderers”), into their respective orbits that the Demiurge had fashioned for them, to look after and create the construct of time, mirroring the eternal and unchanging in a movable model fashioned by the Demiurge himself.  The gods, or planets, as they shone in the sky were mostly made of fire, and were the most divine of all beings that were created, and subsequent to them the Demiurge created creatures of the earth, the air and the water, following the four basic elements of the material universe and each partaking in the divine and intelligent harmony of the universal creation, all moving according to number and making up mankind’s notion of Time.

Time, then, came into existence along with the Heaven, to the end that having been generated together they might also be dissolved together, if ever a dissolution of them should take place; and it was made after the pattern of the Eternal Nature, to the end that it might be as like thereto as possible; for whereas the pattern is existent through all eternity, the copy, on the other hand, is through all time, continually having existed, existing, and being about to exist. Wherefore, as a consequence of this reasoning and design on the part of God, with a view to the generation of Time, the sun and moon and five other stars, which bear the appellation of “planets,” came into existence for the determining and preserving of the numbers of Time. And when God had made the bodies of each of them He placed them in the orbits along which the revolution of the Other was moving, seven orbits for the seven bodies.[4]

After outlining the creation of the heavens and living beings in what Plato refers to as the “operations of Reason”, he then outlines what came into existence via “Necessity”, starting again with the four elements (earth, air, fire and water) which are the basic constituents within the “receptacle” of the universe, the nurse of all Becoming and that which houses the copy of the World Soul. 

Given that these four elements have depth and exist in three dimensional space, Plato, influenced no doubt by the atomicist Democritus and Pythagoreans before him, posits that these basic elements at their core consist of geometrical shapes, of which the triangle is the most “fair”, or most perfect.  The rectangular isosceles triangle and the rectangular scalene are the ones which he uses for the basic building blocks of the elements, for from these, geometrically speaking, all other triangles can be constructed.  In turn from these triangular shapes, he describes the construction of what have come to be known as the Platonic solids, each of which are assigned one of the basic elements.  The solids are the tetrahedron, or pyramid which is associated with fire, and the octahedron which is associated with air, the icosahedron which is associated with water, and the cube which is associated with earth.[5]

[1] Plato, Republic 7.526a. 

See http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.01.0168%3Abook%3D7%3Asection%3D526a

[2] See https://faculty.washington.edu/smcohen/320/timaeus.htm for a good summary of Plato’s cosmology as outlined in the Timaeus.

[3] The actual dimensions, or more properly put lengths, of the substance that was used to create the different circles can be viewed as a slight variant of Pythagoras tetraktys (the numbers 1, 2, 3 and 4 laid out as the dimensions of a triangle in descending order) as Plato uses the same series of digits except a power of 2 for even numbers and power of 3 for odd numbers to create the series, as his basic dimensions for the different circles that are fashioned by the Demiurge to construct the celestial spheres are 1, 2, 4, 8 and 1, 3, 9 and 27 respectively, albeit not in that order.  See Plato Timaeus 34a ff. at http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.01.0180%3Atext%3DTim.%3Asection%3D34a.

[4] Plato, Timaeus 38b-38c.  Plato in Twelve Volumes, Vol. 9 translated by W.R.M. Lamb. Cambridge, MA, Harvard University Press; London, William Heinemann Ltd. 1925.  From http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.01.0180%3Atext%3DTim.%3Asection%3D38c

[5] Timaeus 53c -56c.