Turing Machines and Computing

Another excerpt from Homo Mysticus, from toward the end of the work where the argument is made that man is a (bio-chemical) machine of sorts (ex machina, the subtitle of the work).

The set of coincidences that we will go through in the following journey through Computer Science, Biology (genetics) and ancient Chinese philosophy (Dàodé Jīng) are nothing short of extraordinary and perhaps as profound a discovery as we have seen in our history relative to the (re) bridging of the Sciences – bringing the esoteric, gnosis, back into the intellectual fold as it were, as it was with Aristotle and all the ancients philosophers really.

One must remove the key from the religious texts first, which I believe we have done here. The texts are coded – with basic numbers and an implied Geometry within which the basic construction and structure of the universe can be extracted, inferred if combined with the proper wisdom and approach of course. Those with eyes to see and ears to hear as Jesus tells us.

We’re going to start with Computer Science theory – which I was never really a fan of honestly, it involves computability and run time boundary type problems which are fundamental to computer Science but have applicability really only to the field itself. I liked building stuff. Because it is cool. I would imagine God feels the same way somehow. Operating Systems and HTTP Web Browsers for example were some of the coolest coding I ever did. Basic network and systems infrastructure software is some of the most elegant software on the planet, and as it turns out has significant applicability for modern Cognitive Science. We are large scale computers really, or at least really look like them from a certain perspective, and one of the areas where this connection is established is at the very foundation of the life building system itself actually, in our DNA.

One of these theoretical imperatives you might call it, that underpins Computer Science is one of computability – whether or not a problem is solvable essentially, as well as (and more interestingly from my point of view as a builder) the abstract mechanism by which we can answer this question.

Enter the Turing Machine.[1]

It would appear that (Alan) Turing actually created the notion of the Turing Machine, what he called a ‘logical computing machine’, that in theory could solve all mathematical problems that had an ‘effective’ solution in order to prove that a specific problem was in fact not computable. As sort of an inverse proof by establishing the specific boundaries of computable problems, and their respective ‘effective’ solutions. Once this theoretical logical computing machine was rigorously defined, the notion of the solvability of a mathematical problem – or really any problem capable of being expressed in rigorous mathematical language more or less – was now firmly established on mathematical grounds basically. Computer Science was effectively born, and its connection with Mathematics was firmly established. The graduate school I went to for Computer Science for example was a joint department with Mathematics – the Courant Institute for Mathematical Sciences as it is (still) called. The revolution here was the formalism, and power of the mathematical principles upon which computing as a theoretical notion now rested upon, that computer Science could rest on – as a function of the notion of computability itself.

In other words, if we can establish the boundaries of computability in a mathematically formal way, establish effectively whether or not a problem is solvable by a Turing Machine, computer scientists were now able to change the informal claim that there exists an effective method for obtaining the values in a mathematically solvable function f, by the formal claim that f is a member of S, where S is the set of all possible computable solutions for f. The only way you can make this claim however is of course if you define the intellectual machine that will solve these problems – define the boundaries of set S basically, where again S is the set of computable solutions to a given mathematical equation f.

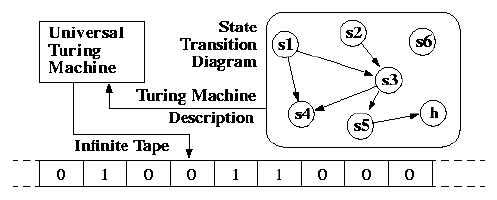
So what is a Turing Machine (TM)? It’s fundamentally a machine (a computer basically but these did not exist at the time that Turing wrote his thesis in the 30s) that reads an (infinite) input tape, value by value and outputs [the result of its calculations] to a theoretical tape or piece of paper, any persistent data store really. The output tape is bound by, a function of really, the input tape of course, and its contents – the result of the solve for function f, can be found on this output tape after the machine is finished ‘processing’, until the inputs are finished basically.

Turing Machine description.[2]

Of course computers are Turing Machines, and given their fundamental binary structure (0 or 1 bits), lend themselves to computability in general given that the list of possible values is well defined, bound as it were between these two bits, and as such has the ability to rest on this type of Computer Science theoretical formalism.[3] What determines how inputs are translated to outputs is the contents of what’s called a Finite State Machine (FSM) which exists inside the Turing Machine and identifies the rules by which one can move from one state to the next. There can be as many of these states, and associated rules, defined in this FSM as long as they are of course finite in number. Any infinite set would have computability problems of course and we are trying to establish the bounds of computing here basically.

The associated figure above shows what this Turing Machine looks like, and of course this is the very intellectual basis for all modern computing. All of it.

What’s fascinating here, again as a builder, is that you can actually build Turing Machines, you can code them. Many of the best software tools out there in the market today have Turing Machines inside them, and this makes them immensely flexible and powerful. Workflow engines are basically Turing Machines, with a specific set of predefined ‘States’, as well as rules for state transition, built into them. Atlassian has a tool called JIRA which has this baked into it’s core. All of the most powerful business applications leverage this concept one way or another.[4]

Turing Machines built on Turing Machines. As above, so below.

[1] We won’t get into the man here much but he in himself has a fascinating life story – Alan Turing that is. One of the code breakers that worked for the British during WWII that I believe Churchill himself attributed with shaving two years off the war. There is a great movie about how this was accomplished, and it’s a great story. Called the Imitation Game starring Benedict Cumberbatch directed by Morten Tyldum (2015). Strongly recommend it.

[2] From Manolis Kamvysselis at MIT: https://web.mit.edu/manoli/turing/www/turing.html.

[3] Part of the problem with create quantum computers is not theoretical, you should be able to build them, but in the problem of measurement at the sub-atomic scale. Turns out entanglement and the measurement problems in quantum physics are in fact practical problems of ‘measurement’ as well, which is required to compute of course. The potential payoffs here though are enormous and this aligns with the current investment. This will be a massive field in the 21^st century, ushering in the next wave of computing.

[4] An actual example of this, with the code to match as well as inputs and output examples, can be found on Manolis Kamvysselis site at https://web.mit.edu/manoli/turing/www/turing.html.